1654. 랜선 자르기 (C#)

문제

• 랜선 자르기 | 실버II (2025년 9월 3일 기준)
• 알고리즘 분류
  • 이분 탐색
  • 매개 변수 탐색

접근

이 문제는 길이가 제각각인 랜선을 잘라내어 길이가 모두 N으로 동일한 랜선을 필요한 만큼 만들때 N의 최대값을 구하는 문제다.

Parametric Search (매개 변수 탐색)

매개 변수 탐색은 최적화 문제를 결정 문제로 변경하여, 이분탐색을 이용해 문제를 해결하는 것이다. 이 문제에서는 문제에서 주어지는 랜선의 최대 길이가 int 최대값으로 주어지기 때문에 단순히 랜선의 길이를 1 늘리고 줄여 탐색하는 방법으로는 제한시간으로 인해 문제를 해결하기 어렵다. 여기에 '이분 탐색'의 개념을 이용해 보는 것이다.

Parametric Search  적용하기

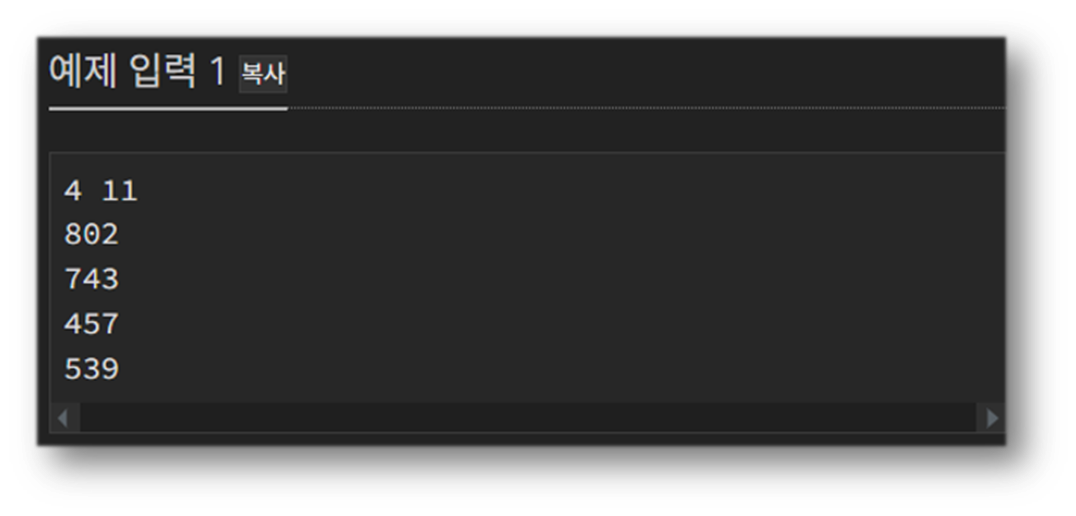
예제 입력을 생각해보자. 갖고있는 랜선의 최대 길이는 802이다. 이때 만들수 있는 랜선 길이 N의 범위는 1-802 라고 생각해 볼 수 있다. 여기서 가장 많은 랜선을 만들 수 있는 랜선의 길이 N의 최대값을 이분 탐색을 이용해 찾는 것이다.

802의 절반인 401부터 시작해본다.401cm 랜선은 몇개를 만들 수 있는가? 5개다. (802에서 2개 + 743에서 1개 + 457에서 1개 + 539에서 1개) 이는 필요한 랜선의 개수인 11개 보다 적으므로 답이 아니다. 그러므로 401보다 긴 랜선은 정답이 아니라는 것을 알 수 있다!

401의 절반인 200을 고려해본다. 4개 + 3개 + 2개 + 2개 로 정확히 11개의 랜선을 만들 수 있다. 문제의 답은 200이 맞지만 여기서 단정할 수 있을까? 단정하기는 어려워 보인다. 하지만 200보다 짧은 랜선은 정답이 아니라는 것을 알 수 있다!

200과 401의 중간인 300을 고려해본다. 2 + 2 + 1 + 1 = 6개로 필요한 랜선의 개수인 11개 보다 작다. 그러므로 300보다 긴 랜선은 정답이 아니라는 것을 알 수 있다

이런식으로 마치 이분탐색을 하는 것 처럼 점차 정답의 범위를 좁혀 나가 최종적으로 최대값 N을 구할 수 있을 것으로 보인다. 이것이 바로 이분탐색의 응용인 매개 변수 탐색이다.

풀이

static void Main(string[] args)
{
    /* 문제의 입력
     * 첫째 줄 : 랜선의 개수 K, 필요한 랜선의 개수 N
     * K 줄에 걸쳐 이미 가지고 있는 각 랜선의 길이가 정수로 입력(<=2^31 -1)
     */
    string[] input = Console.ReadLine().Split(' ');
    long numOfUTP = int.Parse(input[0]); //가지고 있는 랜선의개수
    long numOfReq = int.Parse(input[1]); //필요한 랜선의 개수
    long[] UTPs = new long[numOfUTP]; //가지고 있는 랜선들의 길이

    long start = 1; //parametric search
    long end = 0; //parametric search

    for (int i = 0; i < numOfUTP; i++)
    {
        UTPs[i] = int.Parse(Console.ReadLine());
        end = Math.Max(end, UTPs[i]);
    }

    //Parametric Search
    //최적화 문제 -> 결정 문제
    //이분탐색
    long unit = 0;
    long sum = 0;
    long ans = 0; //answer 변수 추가
    while (start <= end)// while (lo + 1 < hi) 동안
    {
        unit = (start + end) / 2; //mid = (lo + hi) / 2
        sum = 0;
        for(long i = 0; i< numOfUTP; i++) {
            sum += calcUTPCutting(UTPs[i], unit);
        }
        if (sum < numOfReq)
        {
            end = unit - 1;
        }
        else
        {
            start = unit + 1;
            ans = Math.Max(ans, unit); //쵀대값 기록
        }
    }
    System.Console.WriteLine(ans);
}

sum(만들 수 있는 랜선의 개수) 가 문제에서 주어진 필요한 개수(numOfReq)보다 적은 경우 end를 mid-1로 조정한다. 아닌 경우 start를 mid + 1로 조정하고 현재까지 최대 길이를 기록해둔다. 이분 탐색에서는 start, end, mid, 반복 조건을 잘 생각해야 한다. 어느하나라도 잘못될 경우 정답이 나오지 않거나 루프를 탈출하지 못해 시간초과가 날 수 있다.

// 랜선을 단위 길이로 잘라서 몇개가 나오는지 구하는 함수
static long calcUTPCutting(long length,long unit)
{
    return length / unit;
}